
Info zum IFHB e.V.
Das Internationale Forum Historische Bürowelt e.V
(I.F.H.B.) widmet sich der gesamten historischen
Bürotechnik mit den Schwerpunkten mechanischer
Rechenmaschinen und Schreibmaschinen
 .
.
Publikationen: Quartalsweise die Zeitschrift
Historische Bürowelt mit
ausführlichen Fachartikeln, sowie monatliche
Vereinsnachrichten HBw-aktuell.
www.ifhb.de

Zum Rechnen braucht man Ziffern...
...oder einen Abakus.
Der Abakus gehört zu den ältesten bekannten Rechengeräten. Zwischen 2700 und 2300 v. Chr. verwendeten die Sumerer Holz- bzw. Tontafeln mit Spalten, auf die Rechensteine gelegt und verschoben wurden. Dabei verwendete man das Sexagesimalsystem. Den Übergang auf das Dezimalsystem erfolgte erst später durch die Babyloner. Auch die Römer verwendeten eine Art von Abakus.
Das Rechnen mit römischen Zahlen ist ausgesprochen
sperrig. Versuchen Sie mal folgende
Berechnung schriftlich
mit römischen Zahlen durchzuführen:
XIV * XXIV (= 14 * 24)
Ein zentraler Grund ist die fehlende Null.
628 n. Chr. wird urkundlich durch den indischen Astronom und Mathematiker Brahmagupta die Null als vollwertige Ziffer erwähnt.
Gegen Ende des 10. Jahrhunderts erreicht das indisch-arabische Zahlensystem die iberische Halbinsel und verbreitet sich in Europa.
(Bildquelle: Detlef Zerfowski, japanischer Soroban (Abakus))

Das macht nach Adam Ries(e)... (1492 - 1559)
Im Mittelalter diente das dem Abakus ähnelnde Rechenbrett als Rechenhilfsmittel für die vier Grundrechenarten.
Aus dieser Zeit stammen auch die ersten weiter verbreiteten Rechenbücher von Adam Riese, der das Rechnen mit Rechenpfennigen auf Linien, sowie arithmetische Zahlenrechnungen für die Allgemeinheit (d.h. in deutscher und nicht lateinischer Sprache) propagierte.
Dies ist der Ursprung für die in Deutschland bekannte Redewendung ...das macht nach Adam Riese...
(Bildquelle: Adam Ries: Rechnung auff der Linien unnd der Federn/Auff allerley Handtierung, 1550)

Lord John Napier (1550 - 1617) und seine Stäbchen...
Er erfand die nach ihm benannten Napier-Stäbchen (auch Neper-Stäbchen genannt) die für Multiplikation und Division genutzt wurden.

Bildquelle: E. M. Horsburgh:
''Modern instruments and methods of calculation:
Napier Tercentenary Celebration:
Handbook of the
Exhibition of Napier relics and of books
instruments and devices for faciltating
calculation'', 1914.
Die Idee:
Das kleine Ein-Mal-Eins spaltenweise so auf
Holzstäbchen zu schreiben, dass durch
Nebeneinanderlegen entsprechender Stäbchen die
Multiplikation durch einfache Additionen
realisiert werden.
Beispiel: Berechnen von 7 * 8649 = 60543
Wähle aus den Satz der Stäbchen
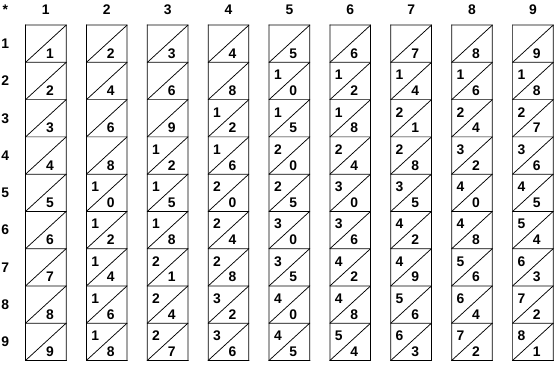 .
.
Wähle aus den Satz der Stäbchen, die
Stäbchen aus, die zu den Ziffern des Multiplikanden gehören.
Hinweis: Es gibt mehrere solcher
Sätze, da ein Multiplikand auch mehrere gleiche Ziffern
besitzen kann.
Lege die ausgewählten Stäbchen
entsprechend der Ziffern des Multiplikanden nebeneinander.
Wähle nun die Zeile die dem
Multiplikator entspricht.
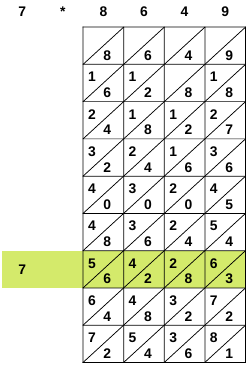 .
.
Von rechts nach links, addiere die
diagonal untereinander stehenden Zahlen, unter
Berücksichtigung eines eventuellen Übertrages aus der
vorherigen Diagonalen.
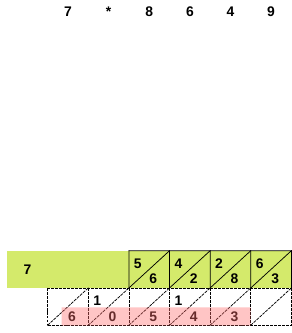 .
.

...und Napiers & Briggs (1561 - 1630) Logarithmen
Im Jahr 1614 entdeckte Lord Napier die Logarithmen, die anschließend ihren Siegeszug im Bereich mathematischer Berechnungen begannen.
Henry Briggs schlug, nach dem intensiven Studium von Napiers Schriften vor, Logarithmen zur Basis 10 (die entsprechend als dekadische bzw. briggsche Logarithmen bezeichnet werden) zu verwenden.
Mit Hilfe von Logarithmen lassen sich
Multiplikationen auf Additionen und
Divisionen auf Subtraktionen zurückführen.
In Formeln ausgedrückt heißt dies
log(a*b) = log(a) + log (b)
bzw. log(a/b) = log(a) - log (b).
Hierdurch werden mathematische Berechnungen deutlich vereinfacht.
Gleichzeitig stellt dieser Zusammenhang die Grundlage für die einige Jahre später erfolgende Erfindung des Rechenschiebers.

Wilhelm Schickard (1592 - 1635) und der 30jährige Krieg
Die weltweit erste mechanische Rechenmaschine die die vier Grundrechenarten beherrschte.
Die erste Maschine ist während des 30jährigen Krieges verloren gegangen. Ein zweites Exemplar, das Schickard für Johannes Kepler (27.12.1571 - 15.11.1630) anfertigen lassen hat, wurde bei einem Brand zerstört.
Basierend auf Zeichnungen und
Beschreibungen von Schickard und Kepler wurde
Ende der 1950er ein funktionsfähiger
Nachbau angefertigt.
 .
.
(Quelle:
Deutsches Museum München. Ein weiterer Nachbau befindet sich im Computermuseum der Universität Stuttgart.)
Mathematisch basiert die Maschine auf dem Prinzip der Napierstäbchen.
(Bildquellen: Wilhelm Schickard / Public domain, Conrad Melperger / Public Domain) (links), https://www.ajhw.co.uk/books/book422/book422.html

Richard Delamain (ca. 1600-1644/1645) und William Oughtred (1574 - 1660) streiten um die Erfindung des Rechenschiebers
Richard Delamain und William Oughtred gelten als Erfinder des Rechenschiebers.
Beide gingen von den Gunter-Skalen aus. Statt mit einem Zirkel Abstände auf einer fest stehende Gunter-Skala abzutragen, ging man dazu über, auf Kreisscheiben mit logarithmischen Skalen mittels Zeigern die Strecken abzutragen.
Zu Lebzeiten von Delamain und Oughtred gab es bereits einen erbitterten Streit darüber, wer den Rechenschieber zu erst erfunden hatte. Obwohl Delamain bereits 1630 das kreisförmige Rechengerät in einer Veröffentlichung mit dem Titel Grammelogia or the Mathematicall Ring beschreibt, geht man heute davon aus, dass Oughtred diese Art von Gerät bereits in den 1620er nutzte, dieses aber erst 1631 veröffentlichte und dabei Delamain des Plagiats beschuldigt. Aus diesem Grund schreibt man heute die Erfindung des Rechenschiebers William Oughtred zu.
Erst später werden Varianten mit gegeneinander verschiebbaren Skalen auf Stäben verwendet.
Dabei basiert der Rechenschieber auf den Napierschen und Briggschen Logarithmen. Logarithmische Skalen werden auf dem sogenannten Rechenschieberkörper und der im Körper verschiebbaren Zunge angebracht.
Hierbei nutzt man aus, dass mittels Logarithmen Multiplikationen auf Additionen zurückgeführt werden können. Die Additionen führt man auf dem Rechenschieber durch hintereinanderfügen (durch Verschieben der Zunge im Rechenschieberkörper) von entsprechenden Strecken auf den Rechenschieberskalen aus.
Es wurden unterschiedliche Arten von Läufern verwendet, die eine oder mehrere Haarlinien besitzen. Hierdurch wurde das Gegenüberstellen von Skalenwerten auf der Zunge und dem Körper, sowie das Ablesen von Ergebnissen erleichtert.
Über die nächsten fast 350 Jahre stellte der Rechenschieber ein zentrales Rechengerät dar, da er einerseits preiswert herstellbar war und aufgrund des geringen Gewichtes an alle Orte mitgenommen werden kann (sogar mit den Apollo-Missionen zum Mond).
(Bildquelle: wikimedia, Wenceslaus Hollar / Public domain

Blaise Pascal (1623 - 1662), Rechnen im Finanzamt
Entwarf eine Maschine für Addition und Subtraktion - die sogenannte Pascaline.
Er entwickelte die Maschine für seinen Vater, der königlicher Kommissar und oberster Steuereinnehmer für die Normandie war.
Die ersten Maschinen konnten nur addieren, spätere auch subtrahieren. Die aufwendige manuelle Fertigung der etwa 50 Exemplare (neun sind noch erhalten) verhindern eine große Verbreitung.
Pascal war auch der Namensgeber für die in den Ende 1980er - Anfang 1990er verbreiteten Programmiersprache.
(Bildquelle: Detlef Zerfowski)

Gottfried Wilhelm Leibniz (1646 - 1716), der Universalgelehrte
Leibniz gilt bereits zu Lebzeiten als einer der ganz großen Universalgelehrten. Als solcher ist er auch der Erfinder der Staffelwalzenrechenmaschine.
Insgesamt wurden drei leicht unterschiedliche Maschinen hergestellt. Die jüngste der Maschine ist erhalten und befindet sich in der Niedersächsischen Landesbibliothek.
Es gibt drei Nachbauten aus den 1920er. Einer davon ist die hier abgebildete Maschine im Deutschen Museum München.
Bei allen Maschinen funktionierte der Zehnerübertrag nicht über alle Stellen korrekt. Erst ein leicht modifizierter Nachbau an der TU Dresden führte zu einer voll funktionsfähigen Maschine.
(Bildquelle: Detlef Zerfowski)

Philipp Matthäus Hahns (1739 - 1790) Tortenrechenmaschinen
Der evangelische Pfarrer Philipp Matthäus Hahn widmete sich neben seinen theologischen Aufgaben ausgiebig dem Bau mechanischer Instrumente.
Neben Sonnenuhren, Teleskopen, Neigungswaagen, Weltmaschinen und auch Rechenmaschinen, die er für Konstruktionsberechnungen der anderen Instrumente benötigte.
Die technologische Grundlage stellte das Staffelwalzenprinzip von Leibniz dar.
Wie auch seine Vorgänger kämpfte Hahn mit dem korrekten Zehnerübertrag durch alle Stellen. Aus diesem Grund dauerte die Entwicklung der ersten tortenförmigen Maschine mehrere Jahre von 1770 an. 1773 existierte ein Prototyp, der erst 1778 vorgestellt wurde.
Hahn baute 5 oder 6 Maschinen dieser Art, von denen zwei erhalten sind.
(Bildquelle: Detlef Zerfowski, Landesmuseum Württemberg Stuttgart)

Charles Xavier Thomas (1785 - 1870), Rechner für Versicherungswesen
...auch Thomas de Colmar genannt,
entwickelte seine Arithmometre auf Grundlage der Staffelwalzen von Leibniz und erhielt dafür 1820 ein Patent zugesprochen.
Es handelt sich dabei um die erste in Serienproduktion gefertigte Maschine, von der in unterschiedlichen Varianten weltweit ca. 1500 mal verkauft wurden.
Später stellten auch andere Hersteller Maschinen nach dem selben Prinzip her. Insbesondere sind die Burkhardt-Arithmometer zu erwähnen, die durch die Firma Arthur Burkhardt & Cie gefertigt wurden. Diese Produktion stellte den Startpunkt der deutschen Rechenmaschinenproduktion in Glashütte/Sachsen dar.
(Bildquelle: Detlef Zerfowski, Thomas-Arithmometre im Deutschen Museum München)
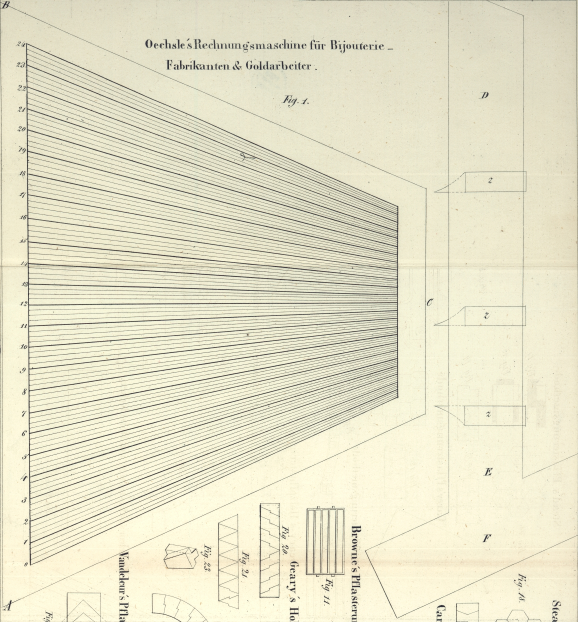
Christian Ferdinand Oechsle (1774 - 1852) Bijouterie-Rechenmaschinen
Rechnungsmaschine für Bijouterie-Fabrikanten und
Goldarbeiter, um Goldlegirungen von jedem Feingehalt
und Mischungsverhältnisse von Kupfer und Silber zu
berechnen.

Bei der ``Rechnungsmaschine'' handelt es sich nicht um eine Maschine, sondern um ein Rechenhilfsmittel mit dem einfach die Anteile der unterschiedlichen Legierungsbestandtteile bestimmt werden konnte.
Mathematische Grundlage der Rechnungsmaschine ist der Strahlensatz, bei dem Streckenverhältnisse bei Parallelverschiebungen erhalten bleiben. Oechsles Erfindung erlaubt zu einer gewünschten Goldqualität (definiert durch spezifische Legierungsanteilen von Gold, Silber und Kupfer), ausgehend von einer vorhandenen Legierung, durch verschieben eines Lineals auf dem Strahlendiagramm ohne Rechnung die hinzuzufügende Menge an Gold, Silber und Kupfer zu bestimmen, um die gewünschte Goldqualität zu erhalten.
(Bildquellen: Dinglers Polytechnisches Journal Band 78, 1840, Seiten 338-344, Tafel 1. Portrait Christian Ferdinand Oechsle: Stadtarchiv Pforzheim StadtA PF S1-29-O-6-P-2.)

Amsler, Miller und Ritter von Hauenfels erfinden das Polarplanimeter
Unabhängig voneinander erfinden Jacob Amsler, A. Miller und Ritter von Hauenfels das Polarplanimeter.
Polarplanimeter werden zur Flächenberechnung von geschlossenen Kurven, also der mathematischen Integration von graphisch vorgegebenen Kurven, benutzt.
Polarplanimeter waren in Vermessungsämtern und -büros ein weitverbreitetes analoges Rechengerät, z.B. zur Berechnung von Grundstücksflächen.
Neben Polarplanimetern gab es eine Vielzahl unterschiedlicher Planimetervarianten, wie z.B.:
Scheibenpolarplanimeter (um höhere
Berechnungsgenauigkeiten zu erzielen),
 .
.
Linearplanimeter (zur Verwendung bei langgestreckten Diagrammen),
Radialplanimeter (zur Auswertung von radial aufgenommenen Messschrieben),
Planimeter für Indikatordiagrammen (zur
Leistungsbestimmung von Dampfmaschinen)
 .
.
Momentenplanimeter zur Bestimmung mehrerer
unterschiedlicher Integralfunktionen für eine
Kurve,
 .
.
Im wissenschaftlichen Sektor kamen
Polarplanimeter mit sogenannten
Harmonischen Analysatoren zur
Fourier-Analyse von vorgegebenen Funktionsgraphen
zum Einsatz. Das nachfolgende Bild zeigt einen
ca. 3,5 x 1,5 Meter großen Aufbau eines 8-fach
harmonischen Analysator der Firma Ott aus dem
Jahr 1941.
Auf der linken Seite des Aufbaus
befinden sich sechs, auf der
rechten Seite zwei Polarplanimeter.
 .
.
Aufgrund der eher ingenieurs- bzw. wissenschaftlichen Anwendung dieser Geräte (Kenntnisse der Integralrechnung sind erforderlich), existiert nur ein relativ kleiner Kreis von Sammlern, die sich hierfür interessieren. Auch in Museen findet man nur sehr selten entsprechend ausgestellte Exemplare.
(Bildquelle: Detlef Zerfowski)

Rechenschieber mit unterschiedlichsten Skalenanordnungen
Die Leistungsfähigkeit und Einsatzgebiete der Rechenschieber wurde durch das verwendete Skalensystem, die Größe und die Materialien bestimmt.
Ein weiteres wichtiges Kriterium war, ob es sich um einen einseitigen oder doppelseitigen Rechenschieber handelte.
Die weitverbreitesten Skalensyteme waren:
System Mannheim:
Um 1850 durch
A. Mannheim (1831-1906) entwickelt,
fand es weite Verbreitung bis in den
zweiten Weltkrieg.
Skalen Vorderseite:
- A (Quadratskala 1...100 auf Rechenschieberkörper),
- B (Quadratskala 1...100 auf Zunge),
- C (Grundskalaa 1..10 auf Zunge),
- D (Grundskalaa 1..10 auf Rechenschieberkörper).
Skalen Zungenrückseite:
- L (Logarithmen bezogen auf D),
- S (Sinus bezogen auf A),
- T (Tangens bezogen auf A),
System Rietz:
1902 durch Max Rietz (1872-1956)
entwickelt, ist das System Rietz bis
zum Ende der Rechenschieberproduktion
die am häufigsten verwendete
Skalenanordnung.
Skalen Vorderseite:
Im Vergleich zum System Mannheim
wurde die Mantissenskala L auf die
Vorderseite geholt und die
Kubikskala K hinzugefügt und die
Sinusskala auf D bezogen.
Außerdem wurde die neue ST Skala
eingeführt, die den nun fehlenden Teil der
Sinusskala abdeckte.
System Log-Log
Einführung doppelt logarithmischen Skalen.
System Darmstadt:
ca. 1934 durch Alwin Walther an der
TH Darmstadt entworfen.
Weiterentwicklung auf Basis Rietz aber
mit stark veränderten Skalenanordnungen,
so dass bei den meisten Berechnungen ein
Wenden der Zunge nicht mehr erforderlich
war.
Die Genauigkeit der Rechenergebnissse wurde
insbesondere durch die Länge der Skalen und damit
durch die Rechenschieberlänge bestimmt.
Die gängigsten Größen waren:
ca. 12 cm (Taschenrechenschieber, häufiges
Werbegeschenke)
ca. 30 cm (die gängiste Variante, die
ungefähr der Höhe eines DIN-A4 Blatts
entsprach)
ca. 50 cm (für genauere Berechnungen, aber
schon schlechter handhabbar).
Um längere Skalen auf kleineren Raum zu realisiern,
wurden
kreisförmige Rechenschieber und
walzenförmige Rechenschieber
verwendet,auf denen eine hohe Anzahl an Skalen
aufgebracht waren, oder
Skalen spiralförmig umliefen.
(Bildquelle: Sammlung Zerfowski)

Eduard Selling (1834 - 1920) war unzufrieden mit dem Arithmometre
Selling war mit der Handhabung der Thomas Arithometre unzufrieden und patentierte eine Multiplikationsmaschine, die 1893 auf der Weltausstellung in Chicago prämiert wurde.
Selling verwendete die Maschine für seine wissenschaftlichen Berechnungen im Rahmen der Zahlentheorie und der Versicherungsmathematik.
Die Maschine besaß als zentrales Element eine Konstruktion nach dem Prinzip der Nürnberger Schere.
Die Maschine erreichte aufgrund der komplizierten Bedienung keine große Verbreitung. Bis 1898 wurden ca. 30 - 40 Maschinen in unterschiedlichen Varianten gefertigt.
(Bildquelle: Detlef Zerfowski)

Hermann Hollerith (1860 - 1929) und die Volkszählung
Das von Hollerith entwickelte System benutzte Lochkarten zur Datenerfassung und -auswertung.
Initial wurde das System zur großflächigen Erfassung und Auswertung medizinischer Daten eingesetzt. Später kam es auch im Rahmen der 11. amerikanische Volkszählung zum Einsatz.
Grundlage der Erfindung war ein ähnlicher Mechanismus mit dem Webstühle für unterschiedliche Stoffmuster gesteuert (heute würde man sagen programmiert).
Aus der Hollerith Company entstand später die auch heute noch bekannte IBM.
(Bildquelle: Von Adam Schuster - Flickr: Proto IBM, CC BY 2.0, Link)
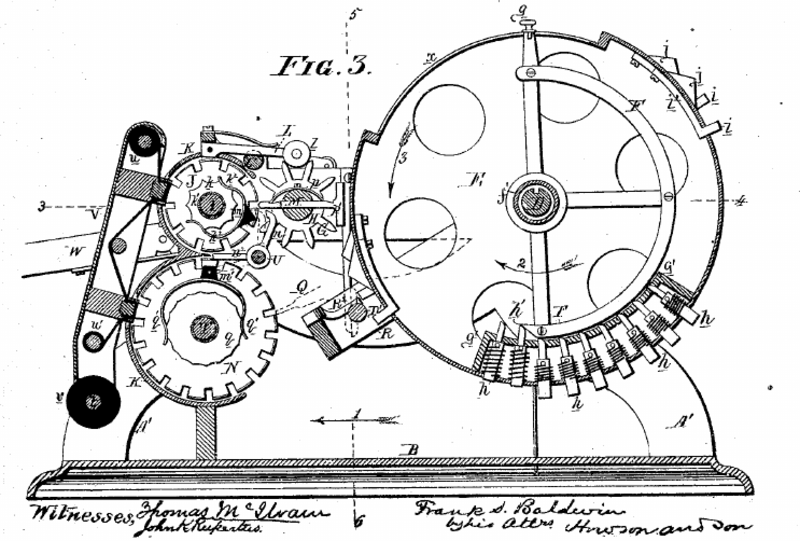
Frank Stephen Baldwin (1838-1925) erfindet das Sprossenrad (erneut)
Bereits lange bevor Baldwin gab es Ideen zu einem Sprossenradmechanismus.
Bei einem Sprossenrad handelt es sich um ein Rad aus dem 1 bis 9 Zähne radial herausgeschoben werden können. In Baldwins Lösung werden die Zähne über die Federn wieder in das Rad zurück gezogen.
So entwarf bereits Gottfried Wilhelm Leibniz (1646-1716) ein Sprossenrad, verwendete später aber das Staffelwalzenprinzip.
Giovanni Poleni (1683-1761) ersann für seine hölzerne Rechenmaschine ein Klappsprossenrad.
Antonius Braun (1686-1728) konstruierte im Jahr vor seinem Tod ebenfalls eine Sprossenradmaschine, die heute im Technik Museum Wien steht.
Didier Roth entwarf 1841 und 1848 Maschinen mit diesem Mechanismus.
1848 schließlich patentierte der Engländer David Isaac Wertheimber ein Sprossenrad, welches bereits große Ähnlichkeit mit Baldwins Sprossenrad besitzt.

Willgodt Theophil Odhner (1845 - 1905) baut ebenfalls auf das Sprossenrad
Auch Willgodt Theophil Odhner war mit den Thomasschen-Staffelwalzenmaschinen unzufrieden und erstellte bereits 1874 einen manuell gefertigten Prototypen einer Sprossenradrechenmaschine
 .
.
(Quelle: Ernst Martin,
Die Rechenmaschine und ihre
Entwicklungsgeschichte, 1925),
1878 erfolgte die Patentierung dieser Maschine.
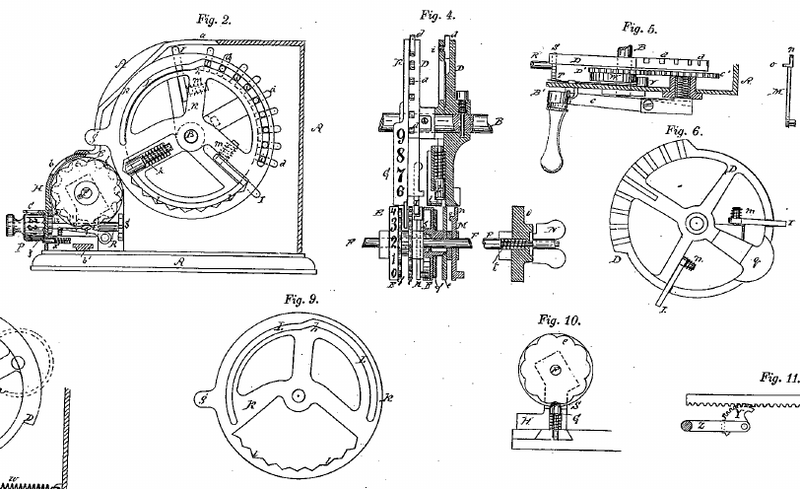
Bei Odhners Sprossenrad werden
mittels eines Schlitzes (Fig. 9) die
Zähne (Fig. 2) radial
herausgeschoben.
 .
.
(Auszug aus dem deutschen Patent 7393
aus dem Jahr 1878).
Mangels Geldgeber wurden die frühen Patente nicht als Serienprodukte umgesetzt. Dies geschah erst ab 1890.
Zwei Jahre später erwarb Grimme, Natalis & Co (Brunsviga) die Lizenzrechte für Deutschland, Belgien und die Schweiz.
Willgodt Odhners Rechenmaschinenfabrik und deren Rechtsnachfolger produzieren bis 1970 mehr als 1 Millionen Rechenmaschinen unterschiedlichster Art.

Die Millionär - mit direkter Multiplikation
Die Millionär ist die erste erfolgreiche, serienmäßig produzierte Rechenmaschine mit direkter Multiplikation.
Otto Steiger (1858 - 1923) erfand das Grundprinzip (patentiert 1892), bei dem das kleine Ein-Mal-Eins in Form von Stäben auf einer Grundplatte kodiert war.
Z.B. musste bei einer Multiplikation mit der Zahl 8 nicht mehr, wie bei den vorherigen Maschinen, acht Mal die Kurbel gedreht werden, sondern man stellte den Operanden auf 8 und drehte die Kurbel nur einmal.
Von der Maschine wurden in unterschiedlichen Varianten 4655 Exemplare gebaut.
Zu Beginn des 20 Jahrhunderts war der Preis der Maschine vergleichbar mit dem Preis eines Autos.
(Bildquelle: Sammlung Detlef Zerfowski)

Saldieren und Buchhaltung mit dem Comptometer
Für die Buchhaltung im Büro wurden anfänglich häufig keine (relativ teuren) Vierspeziesmaschinen eingesetzt.
Im alltäglichen Geschäft mussten umfangreiche Zahlenkolonnen addiert bzw. subtrahiert werden. Dieses wurde mittels Zweispeziesmaschinen durchgführt, die lediglich Addition und Subtraktion, aber keine Multiplikation und Division beherrschten.
Im obigen Bild sind 90 Comptometer-Arbeitsplätze
zu sehen, die im zwei-Schicht-Betrieb die
Steuereinnahmen für das Los Angelos County im Juni
1935 berechnen.
Man beachte die Größe der Bücher und man
stelle sich den Lärm der parallel betriebenen
Comptometer vor!
Für diese intensive Nutzung waren die recht
schweren, aber robusten Comptometer ideal.
Diese Maschine wurde von
der amerikanischen Firma
Felt & Tarrant Mfg. Company gefertigt und
weltweit in großen Mengen vertrieben.
 .
.
Es gab auch eine Vielzahl von Anbietern,
die einfachere Addierer in den Markt brachten,
wie die abgebildete Contex.
 .
.
(Bildquellen (von oben nach unten): Comptometer News, Vol. 8, Nr. 1, Februar 1836. Comptometer und Contex: Sammlung Detlef Zerfowski)

Volltastenmaschinen unter Strom
Neben den Sprossenradmaschinen entwickelten sich auch die Staffelwalzenmaschinen weiter.
Neben Volltastaturen, zog auch der elektrische Strom in die Maschinen ein. Dabei wurde anfangs lediglich die manuelle Betätigung der Maschine durch einen elektrischen Motor ersetzt.
Spätere Maschinen führten komplexere Operationen automatisch, aber vollständig mechanisch durch.
Es handelt sich dabei um elektrische, aber nicht elektronische Maschinen.
(Bildquelle: Detlef Zerfowski, Archimedes DEaD 20 der ArchimedeS Werke Reinhold Pöthig, Glashütte/Sachsen, gefertigt in der Zeit von 1927 bis 1940)

Brunsviga und die Rechenmaschinen-Großserienproduktion
Brunsviga Maschinenwerke AG, war eine der Weltmarktführer für Vierspeziesrechenmaschinen.
1871 wurde die Firma unter dem Namen Grimme, Natalis & Co. gegründet. Ursprünglich wurden unter anderem Öfen und Nähmaschinen gefertigt und erst später vollständig auf die Rechenmaschinenproduktion fokussiert.
Aufgrund des Erfolgs der Brunsviga Rechenmaschinen wurde 1927 der Name Brunsviga in den Firmennamen aufgenommen. 1959 ging das Firmenvermögen in der Olympiawerke AG auf und 1979 wurden das Olympiawerk geschlossen.
Vierspeziesmaschinen beherschten alle vier Grundrechenarten: Addition, Subtraktion, Multiplikation und Division.
Brunsviga hatte eine große Modellpalette vorzugsweise basierend auf dem Sprossenradprinzip.
Initial war der Bedarf an Rechenmaschinen sehr niedrig. Vermessungsämter waren die Hauptabnehmer. Die Brunsviga-Maschinen ebneten mit einem deutlich niedrigeren Preis (25% des Preises eines Burkhardt Arithometers) den Markt für andere Anwendungsgebiete.
Die Brunsviga-Rechenmaschinen wurden insbesondere wegen ihrer Robustheit geschätzt und wurde in allen erdenklichen Anwendungsfällen eingesetzt.
In Summme wurden mehr als 1/2 Millionen Brunsviga Rechenmaschinen gefertigt.

Doppelrechenmaschinen: High-Performance Computing ohne Strom
Auch in der Mitte des 20. Jahrhunderts wurde auf Effizienz geachtet. So wurden für spezielle Anwendungsgebiete optimierte Rechenmaschinen entwickelt. Insbesondere das Vermessungswesen war in dieser Zeit ein Bereich, der die Weiterentwicklung der Rechentechnik vorantrieb.
Speziell für die umfangreichen Koordinatenberechnungen wurden sogenannte Doppel- und sogar Dreifach-Rechenmaschinen verwendet.
Neben Brunsviga baute auch das Rastatter Thales-Werk entsprechende Maschinen, wie die im Bild dargestellte Thales-Geo. Auf dem amerikanischen Markt baute z.B. Marchant entprechende Maschinen.
(Bildquelle: Detlef Zerfowski)

Curt Herzstark (1902 - 1988) und seine Pfeffermühle Curta
In keiner Rechenmaschinensammlung darf die kleine Curta-Rechenmaschine fehlen.
Dabei handelt es sich um die kleinste (Typ I mit 85 mm Höhe und einem Durchmesser von 53 mm) serienmäßig hergestellte mechanische Rechenmaschine, die alle vier Grundrechenarten beherrschte.
Die Ideen für die Maschine ließ sich Herzstark bereits in den 1930er Jahren patentieren, konnte diese aber auf Grund des Krieges nicht ausführen.
Als Halbjude wurde Curt Herzstark von den Nationalsozialisten gefangen genommen und später in das Konzentrationslager Buchenwald deportiert.
Nur durch einen glücklichen Umstand, wurde es ihm erlaubt, im Konzentrationslager an seiner Erfindung weiterzuarbeiten und entsprechende Konstruktionszeichnungen zu erstellen.
Mit diesen Unterlagen war es ihm möglich von 1947 an, mit dem in Liechtenstein ansässigem Unternehmen Contina AG, die Curta zu fertigen.
Im Zeitraum von 1947 bis 1972 wurden circa 140000 Exemplare in zwei Varianten gefertigt.
(Bildquelle: Sammlung Detlef Zerfowski)

Konrad Zuse (1910-1995) und der erste Computer
Zuse baute während des Zweiten Weltkriegs in seiner Berliner Wohnung den ersten freiprogrammierbaren Computer.
Seine Motivation für den Bau eines solchen Rechners lag darin, immer wiederkehrende Berechnungen im Bauingenieurswesen automatisiert ablaufen zu lassen.
Dabei verwendete er das Binärzahlensystem. Der rein mechanisch aufgebaute Computer hatte bereits zentrale Architekturelemente zukünftiger Computer. So besaß er bereits ein Ein-Ausgabewerk, ein Rechenwerk und ein Speicherwerk.
Mit der Z3 (1941) baute Zuse den ersten funktionsfähigen Computer der Welt. Dabei verwendete er Relais der Telekommunikationsindustrie, statt die rein mechanischen Umsetzung der Z1.
Die Originale der Z1, Z2 und Z3 wurden während der Bombenangriffe auf Berlin zerstört.
Zuse erstellte mit etlichen Helfern eine Rekonstruktion der Z1.
Spätere Maschinen z.B.die Z11 wurden intensiv in Vermessungsämtern eingesetzt.
1965 musste Zuse wegen Überschuldung seine Anteile an seinem Unternehmen veräussern.
(Bildquelle: Detlef Zerfowski, Aufnahme des Z1-Nachbaus im Musuem für Verkehr und Technik, heute Deutsches Technikmuseum Berlin.)

Der HP-35 versetzt dem mechanischen Rechnen den Todesstoß
Der erste technisch-wissenschaftlichen Taschenrechner beendet die Ära des mechanischen Rechnens.
Insbesondere besaß der Rechner trigonometrische, sowie logarithmische und Exponential-Funktionen.
Trotz des hohen Preises von 395 US-Dollar zur Markteinführung in den USA, wurde der HP-35 ein unerwarteter Verkaufsschlager, der die Ära der Rechenschieber und des mechanischen Rechnens überhaupt abrupt beendete.
(Bildquelle: Detlef Zerfowski (links), Wikimedia (rechts).

Wer sorgt dafür, dass dieses Wissen nicht verloren geht?
Weltweit gibt es mehrere Vereine die im Bereich
mechanische Rechnen
das Wissen zusammentragen und konservieren,
das Themengebiet erforschen,
defekte Maschinen wieder zum Leben erwecken und
das mechanische Rechnen im Gedächtnis der
Gesellschaft halten.
Nachfolgend einige dieser Vereine/Organisationen
mit entsprechenden Kontaktdaten.
Das Internationale Forum Historische Bürowelt e.V
(I.F.H.B.) widmet sich der gesamten historischen
Bürotechnik mit den Schwerpunkten mechanischer
Rechenmaschinen und Schreibmaschinen
 .
.
Publikationen: Quartalsweise die Zeitschrift
Historische Bürowelt mit
ausführlichen Fachartikeln, sowie monatliche
Vereinsnachrichten HBw-aktuell.
www.ifhb.de
Die Oughtred Society ist eine in Amerika ansässige
englischsprachige internationale
Sammlergemeinschaft mit dem
Schwerpunktthema Rechenschieber, aber auch anderen
mechanischen Rechengeräten.
 .
.
Publikationen: 2 x pro Jahr das
Journal of the Oughtred Society
mit ausführlichen Fachartikeln.
Internet
Die United Kingdom Slide Rule Circle
(UKSRC) ist ebenfalls englischsprachig, aber sehr
international aufgestellt.
 .
.
Publikationen: 1 x pro Jahr die umfangreiche
Slide Rule Gazette
mit ausführlichen Fachartikeln
und das quartalsweise Blättchen
SkidStick.
www.uksrc.org.uk
Die deutschsprachigen Rechenschiebersammler
Publikationen: Artikel auf der Internetseite
 .
.
www.rechenschieber.org